The average rate of change for the function f(x) can be calculated from the following equation
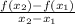
By applying the last formula on the given equations
(1) the first function f
from the table f(3π/2) = -2 and f(2π) = 0
∴ The average rate of f =
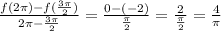
(2) the second function g(x)
from the graph g(3π/2) = -2 and g(2π) = 0
∴ The average rate of g =
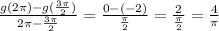
(3) the third function h(x) = 6 sin x +1
∴ h(3π/2) = 6 sin (3π/2) + 1 = 6 *(-1) + 1 = -5
h(2π) = 6 sin (2π) + 1 = 6 * 0 + 1 = 1
∴ The average rate of h =

By comparing the results, The
function which has the greatest rate of change is h(x)
So, the correct answer is option C) h(x)