Question

At the beginning of an environmental study a forest cover an area of 1500 km second power since then this area has decreased by 4.8% each year let T be the number of years since the start of the study letter y b the area that the forest covers in km to the second power write an exponential function showing the relationship between Y&T

Answer 1

`y=1500(0.952)^(t)`

Explanation:

Explicit formula of an exponential function is given by

`A_(t)=A_(0)(b)^(t)`

`A_(t)` = Area covered by the forest after time t

`A_(0)` = Initial area covered by the forest

b = (1 - r)

and r = rate of decay of the forest area

t = time in years

`A_(t)=1500(1-0.048)^(t)`

`y=1500(0.952)^(t)`

Therefore, function representing relationship between y and t will be

`y=1500(0.952)^(t)`

Answer 2

The general exponential equation modelling the change per year in a value is given as:


`A= A_(o)(1-x)^(t)`

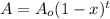
Here,
A₀ is the original amount
A is the amount after t years
x is the change per year. For decreasing values, x will be negative
t is the number of years.

In the given case, the original value of Area is 1500. The change per year is 4.8%, in decimal this equals 0.048. Since the area is decreasing the value of x will be - 0.048.

The area Y that the forest covers after t years can be written as:


`Y=1500(1-0.048)^(t) \\ \\ Y=1500(0.952)^(t)`

The above equation shows the relation between the forest area and the number of years since the environmental study.