Question

What is the length of segment AC

Answer 1

10

Explanation:

I just took the quiz on edge

Answer 2

To find the length of segment AC, we must find the total rise and total run between the two points.

Point C is located at (-5, 5). Point A is located at (3,-1). To find the rise, subtract the y-value of A from the y-value of C:


`5 - (-1) = 6`

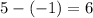
The rise of this segment is 6.

To find the run, subtract the x-value of A from the x-value of C:


`3 - (-5) = 8`

The run of this segment is 8.

We can use the Pythagorean Theorem to find the length of this segment. The theorem uses the following formula:


`a^(2) + b^(2) = c^(2)`

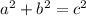
The segment represents the hypotenuse, and the rise and run represent the legs of this segment. We know that the two legs' lengths are 6 and 8, so plug them into the equation:


`6^(2) + 8^(2) = c^(2)`

`36 + 64 = c^(2)`

`100 = c^(2)`

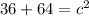
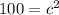
Square root both sides to get c by itself:


`√(100) = 10`

`c = 10`

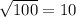
The length of segment AC is 10.