Question

What is the cube root of 27x18? 3x6 3x9 9x6 9x9

Answer 1

3x6 would be your answer

Step-by-step explanation:

Answer 2

A is the correct option.

Step-by-step explanation:

We have to find the cube root of
`27x^(18)`

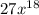
In order to find the cube root of the expression, we find the factors of 27.

`27= 3 * 3* 3= 3^3`

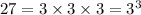
Also x^18 can be written as

`x^(18)=(x^6)^3`

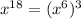
Replace the given expression with these values, we get

`\sqrt[3]{27x^(18)} =\sqrt[3]{3^3 \cdot (x^6)^3 }`

Now, we have the formula,

`\sqrt[n]{x^n} =x`

Using this formula, the cube with the cube root got cancelled and we are left with

`\sqrt[3]{27x^(18)} = 3\cdot x^6`

Therefore, the cube root of 27x^18 is 3x^6.

A is the correct option.