Question

The weight of a radioactive isotope was 96 grams at the start of an experiment. After one hour, the weight of the isotope was half of its initial weight. After two hours, the weight of the isotope was half of its weight the previous hour. If this pattern continues, which of the following graphs represents the weight of the radioactive isotope over time?

Answer 1

Answer: Initial Weight = W₁ = 96

Change factor = 1/2 = 0.5

Explanation:

Answer 2

The starting weight of the radioactive isotope = 96 grams

Weight after one hour is half of the starting weight. So the weight of the radioactive isotope after 1 hour = 48 grams

After 2 hours the weight is half as compared to the weight after previous hour. So weight after 2 hours = 24 grams.

This means, after every hour the weight is being halved. The half life of radioactive isotope is one hour.

Since after every hour, the weight is being halved, the weight of the isotope can be modeled by an exponential equation.

So,

Initial Weight = W₁ = 96
Change factor = 1/2 = 0.5

The general equation of the sequence will be:


`\\ \\ W_(t)=96(0.5)^(t)`

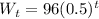
Here t represents the number of hours. Using various values of t we can find the weight of the radioactive isotope at that time.

We can plot the sequence using the above equation. The graph is attached below.