Answer:
∠EAB = 81°
Explanation:
Given :

Tangent = EF
Chord = AB
To Find: ∠EAB
Solution :
We will use Tangent-Chord Angle Theorem
Tangent-Chord Angle Theorem : An Angle formed by a chord and a tangent that intersect on a circle is half the measure of the intercepted arc
Angle formed by a chord and a tangent that intersect on a circle =∠EAB
Intercepted arc =

So, by theorem
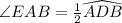
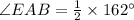
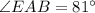
Hence the measure of ∠EAB is 81°