Determine the nature of the roots: 4x^2 + 32x + 64 = 0 a. no real solutions b. a unique real solution c. two distinct real solutions d. cannot be determined

Question

asked Aug 25, 2019 130k views

2 Answers

Kresimir Pendic · Answer 1 · 2019-08-30T19:34:50+0000

Answer:

b. a unique real solution

Explanation:

A quadratic equation ax² + bx + c = 0 ,

Has two distinct real roots,

If discriminant,
D=b^2 - 4ac > 1

Has two equal real roots,

If D = 0,

Has two imaginary roots or no real roots,

if D < 1,

Here. the given qudratic equation,

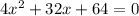
4x^2 + 32x + 64=0

By comparing,

a = 4, b = 32, c = 64,

$\implies D = 32^2 - 4* 4* 64 = 1024 - 1024 = 0$

Hence, the equation has two equal real roots or a unique real solution.

i.e. OPTION 'b' is correct.