Question

Which system represents this graph of linear inequalities?

Answer 1

The continuous line is y = x + 3 and te inequality would be y <= x + 3

The dotted line represents the equation y = -x - 4 and inequality would be
y < - x - 4

The correct choice is the third one.

Answer 2

The right answer is the third:

`\left \{ {{y\leq x+3} \atop {y<-x-4}} \right.`

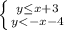
Explanation:

The continuous line is the graph of the function y=x+3.

If we check a any point in the colored area, the inequality must be true.

For example: Point(-5;-5)

We replace the values in the inequality:

y≤x+3

-5 ≤ -5 + 3

-5 ≤ -2

The point fatisfies the inequality.

Secondly, the non-continuous line is the graph of the function y= -x - 4

The line is dotted because the points in the line y= -x - 4 are not included by the inequality.

We check the same point in the colored area.

Point(-5;-5)

y <-x-4

-5 < -(-5) - 4

-5 < 5 - 4

-5 < 1

The point satisfies the inequality, so the point of the area is included by the inequality.