First, we need to find the length of the other two sides of the triangle using pythagorean theorem: the sum of the squares of the perpendicular sides (base and height) is equal to the square of the hypotenuse). For an instance, s represents the length of base/height.
a² + a² = h²
2a² = 72²
2a² = 5,184
a² = 5,184/2
a² = 2,592
a² = 1,296 × 2
a =
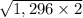
a = 36√2
Second, find the surface area
The surface of prism consists of two bases and lateral sides.
sa = 2 base area + 3 lateral sides
sa = (2 × 1/2 × base of triangle × height of triangle) + perimeter of triangle × height of prism
sa = (2 × 1/2 × 36√2 × 36√2) + (36√2+36√2+72) × 7
sa = 2,592 + (72√2 + 72) × 7
sa = 2,592 + 72(√2 + 1) × 7
sa = 2,592 + 504 (√2 + 1)
sa = 2,592 + 504 (2,4142..)
sa = 2,592 + 1,216.7636
sa = 3,808.7636
to the nearest tenth
sa = 3,808.8 cm²
The surface area is 3,808.8 cm²