Question

A skydiver slows down from 54 m/s to 4 m/s by opening his parachute. this change takes 0.75 seconds. what is the skydiver's acceleration

Answer 1

The acceleration of the skydiver is given by:

`a= (v_f-v_i)/(t)`
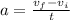
where

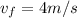
`v_f=4 m/s` is the final velocity of the skydiver

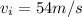
`v_i=54 m/s` is the initial velocity of the skydiver

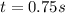
`t=0.75 s` is the time taken for the change of speed

Substituting the numbers into the equation, we find the skydiver's acceleration:

`a= (4 m/s-54 m/s)/(0.75 s) =-66.7 m/s^2`
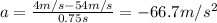
where the negative sign means it is a deceleration.