Question

Select the rational expression that is equivalent to the given expression below.

4 / x - 3

A.) x + 2 / x - 3 ÷ 4 / x + 2
B.) x + 2 / x - 3 · 4 / x + 2
C.) x + 2 / x - 3 - 4 / x + 2
D.) x + 2 / x - 3 + 4 / x + 2

Answer 1

`B.)\ \ (4)/(x-3)`

`(x+2)/(x-3)\cdot(4)/(x+2)\\\\=((x+2)(4))/((x-3)(x+2))\qquad\text{cancel}\ (x+2)\\\\=(4)/(x-3)`

Answer 2

For this case we have the following expression:

`\frac {4} {x-3}`

We must multiply the expression given by the same factor in the numerator and the denominator.

We have then:

`\frac {4} {x-3} \frac {x + 2} {x + 2}`

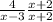
Then, rewriting the given expression we have:

`\frac {x + 2} {x-3} \frac {4} {x + 2}`

Answer:

The rational expression that is equivalent to the given expression is:

`\frac {x + 2} {x-3} \frac {4} {x + 2}`

Option B