Question

What is the simplified base of the function f(x) = 1/4 cubed root of 108

Answer 1

1.19

Explanation:

We are given that a function

f(x)=
`(1)/(4)` cube root of 108

We have to find the simplified base of the given function

`f(x)=(1)/(4)\[tex]\sqrt[3]{108}`

`f(x)=(1)/(4)\sqrt[3]{3*3*3*2*2}`

`f(x)=(1)/(4)* 3\sqrt[3]{4}`

When we finding cube root by the prime factorization formula then we fins prime factors of given number and then we make pair of three same factor then that single number comes out of cube root.

`f(x)=(3*1.587)/(4)`

`f(x)=(4.761)/(4)=1.19025`

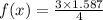
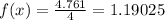
The base of simplified base of function is 1.19.

Answer :1.19

Answer 2

Looks like you want the base of f(x) = ∛(108). To answer this question, you must find the largest perfect cube factor of 108. Make a table of values of cubes:

x x^3

1 1
2 8
3 27
4 64
5 125
6 216

27 is the only perfect cube that divides into 108 without a remainder.

Therefore, f(x) = (1/4)∛(108) = (1/4) [ ∛(27)*∛4 ] = (1/4)*3*∛(4) (answer)