Question

Ben bought 8 fairy sodas and 5 fairy hotdogs and spent $30.75 fairy dollars. Holly bought 7 fairy sodas and 6 fairy hotdogs and spent $33 fairy dollars? (This is systems)

Answer 1

Fairy hotdog cost 3.75, while a fairy soda costs $1.50.

Answer 2

Set up the system of equations:


`8x + 5y = 30.75`

`7x + 6y = 33`

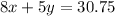
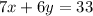
We'll use elimination to solve this system of equations.

Take the coefficients for y in both problems. Multiply one of them by -1:


`5 * -1 = -5`

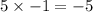
Since this coefficient is taken from the first problem, we'll multiply the entire second problem by this negative coefficient:


`(7x + 6y = 33) * -5 = -35x - 30y = -165`

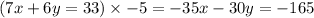
Take the coefficient for y in the second problem and multiply the entire first problem by that coefficient:


`(8x + 5y = 30.75) * 6 = 48x + 30y = 184.50`

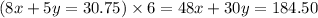
Your system should now look like this:


`48x + 30y = 184.50`

`-35x - 30y = -165`

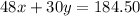
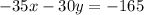
Combine these two equations to cancel out y:


`13x = 19.50`

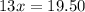
Divide both sides by 5 to get x by itself:


`x = 1.5`

A fairy soda costs $1.50.

Because we know the value of one of the variables, we can plug it into one of the equations:


`8(1.5) + 5y = 30.75`

`12 + 5y = 30.75`

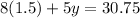
Subtract 12 from both sides:


`5y = 18.75`

Divide both sides by 5 to get y by itself:


`y = 3.75`

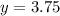A fairy hotdog costs $3.75.