Question

(PLEASE ANSWER: TIMED)The intensity, or loudness, of a sound can be measured in decibels (dB), according to the equation I(dB)=10log[1/10], where I &/ the intensity of a given sound and I0 is the threshold of a hearing intensity. What is the intensity, in decibles, [I(dB)], when I=10^8(I0)? Round to the nearest whole number.

(Refer to photo for equations)
A.8
B.9
C.19
D.80

Answer 1

D) 80

Explanation:

Answer 2

For this case we have the following equation:

`l(dB) = 10log( (l)/(lo) )`
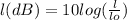
We must replace the following value in the equation:

`l = 10^8lo`
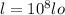
Substituting we have:

`l(dB) = 10log( (10^8lo)/(lo) )`
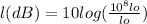
Simplifying the given expression we have:

`l(dB) = 10log(10^8)`
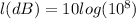
Then, using logarithm properties in base 10, we can rewrite the expression:

`l(dB) = 10(8)`
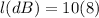
Finally, making the product, the result is:

`l(dB) = 80`
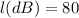Answer:

`l(dB) = 80`
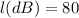option 4