Question

Need help!

The values in the table represent a linear function. What is the common difference of the associated arithmetic sequence?

X Y
1 7
2 26
3 45
4 64
5 83

Choices:
A. 24
B. 19
C. 1
D. 38

Answer 1

In an arithmetic sequence, each number is the previous number plus a certain constant. This constant is the common difference. We can find it by taking any number and subtracting the previous number from it. In this case, 26 - 7 = 19 and 45 - 26 = 19. So the answer is B.

Answer 2

Answer: B. 19

Explanation:

Given: The values in the table represent a linear function.

We know that common difference in A.P. = difference between consecutive terms in the sequence.

Thus, the common difference =
`y_2-y_1=26-7=19`

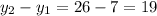
Similarly we can check for the other terms as

`y_3-y_2=45-26=19`

`y_4-y_3=64-45=19`

`y_5-y_4=83-64=19`

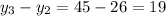
Therefore, option B is correct, the common difference of the A.P.= 19.