Answer:
4 seconds
Step-by-step explanation:
We have the following data for this exercise :
A 20.0 kg mass ⇒
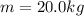
A velocity of +
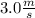 ⇒ The module of this vector is the speed ⇒ We have and initial speed of
⇒ The module of this vector is the speed ⇒ We have and initial speed of
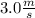
And a constant force F with a value of 15.0 N ⇒
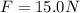
Let's start finding the acceleration that this force applies over the mass.
We can write the following equation :

Where a is the acceleration over the mass ''m'' due to the force F.
Using this equation we can find the acceleration
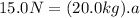
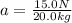
The unit N is equivalent to
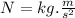
⇒
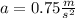
Now in order to find the time, we are going to use the following cinematic equation :
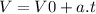
Where V is the speed, V0 is the initial speed and t is the time
We want the mass to stop ⇒
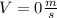
We also know the initial speed
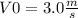
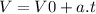
 (I)
(I)
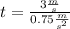
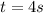
The force must act 4 seconds to stop the mass.
We add a ''-'' in equation (I) because the acceleration is opposite to the movement because it is stopping the mass.