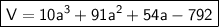Question

The volume of a rectangular prism is given by the formula V = lwh, where l is the length of the prism, w is the width, and h is the height. Suppose a box in the shape of a rectangular prism has length (2a + 11), width (5a – 12), and height (a + 6). Which expression represents the volume of the box?

Answer 1

Just plug the measurements into the formula.


`\sf V=lwh`


`\sf V=(2a+11)(5a-12)(a+6)`

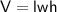
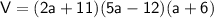
Distribute the first two parentheses. Multiply every term in the first parenthesis to every term in the second parenthesis.


`\sf V=(10a^2-24a+55a-132)(a+6)`

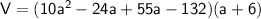
Simplify, combine like terms:


`\sf V=(10a^2+31a-132)(a+6)`

Distribute again. Multiply ever term in the first parenthesis to every term in the second:


`\sf V=10a^3+60a^2+31a^2+186a-132a-792`

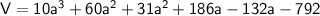
Combine like terms:


`\boxed{\sf V=10a^3+91a^2+54a-792}`