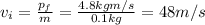Question

Projectiles that strike objects are good examples of inelastic collisions. A 0.1 kg nail driven by a gas powered nail driver collides in an inelastic collision with a 10 kg block of wood at rest. The total momentum of the system after the collision is 4.8 kg · m/s. Round your answers to two significant digits. The velocity of the nail and block after the collision is calculated to be m/s. The expected velocity of the nail prior to the collision is m/s.

Answer 1

Projectiles that strike objects are good examples of inelastic collisions. A 0.1 kg nail driven by a gas powered nail driver collides in an inelastic collision with a 10 kg block of wood at rest. The total momentum of the system after the collision is 4.8 kg · m/s. Round your answers to two significant digits.

The velocity of the nail and block after the collision is calculated to be

0.48

m/s.

The expected velocity of the nail prior to the collision is

48

m/s.

Answer 2

In an inelastic collision, only momentum is conserved, while energy is not conserved.

1) Velocity of the nail and the block after the collision
This can be found by using the total momentum after the collisions:

`p_f=(m+M)v_f=4.8 kg m/s`
where
m=0.1 kg is the mass of the nail
M=10 kg is the mass of the block of wood
Rearranging the formula, we find
`v_f`, the velocity of the nail and the block after the collision:

`v_f= (p_f)/(m+M)= (4.8 kg m/s)/(0.1 kg+10 kg)= 0.48 m/s`

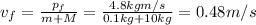
2) The velocity of the nail before the collision can be found by using the conservation of momentum. In fact, the total momentum before the collision is given only by the nail (since the block is at rest), and it must be equal to the total momentum after the collision:

`p_i = mv_i = p_f`
Rearranging the formula, we can find
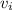
`v_i`, the velocity of the nail before the collision:

`v_i = (p_f)/(m)= (4.8 kg m/s)/(0.1 kg)=48 m/s`