Answer:
R = (-∞,∞)
Explanation:
The given function is
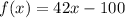
As you can notice, it's a linear function, and it's written in slope-intercept form. So, from this expression we can deduct that the slope is 42 and the y-intercept is at -100. We deduct this information, because of the form
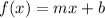
Where
 is the slope and
is the slope and
 is the y-intercept, which in this case are
is the y-intercept, which in this case are
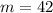 and
and
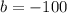 .
.
An important characteristic of linear function is that they domain and range sets are always all real numbers, the function is not restricted.
Therefore, the range of the given function is
R = (-∞,∞)