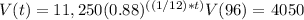Question

A motorcycle is depreciating at 12% per year, every year. A student's $11,250 motorcycle depreciating at this rate can be modeled by the equation V(t) = 11,250(0.88)t. What is an equivalent equation for this vehicle as a monthly depreciation and, using this equation, what is the motorcycle worth (rounded to the nearest hundred dollar) 8 years after purchase?

Answer 1

For this case we have an equation of the form:

`y = A (b) ^ t`
Where,
A: initial amount
b: decrease rate
t: time
In this case we have the following equation:

`V (t) = 11,250 (0.88) ^ t`
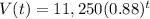
Where,
t: number of years
Rewriting for the number of months we have:

`V (t) = 11,250 (0.88) ^ {((1/12) * t)}`
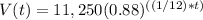
Where,
t: number of months
For 8 years (96 months) we have:

`V (96) = 11.250 (0.88) ^ {((1/12) * 96)} V (96) = 4045.888404`
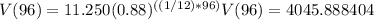
round to the nearest hundred dollar:
V (96) = $ 4050
Answer:

`V (t) = 11,250 (0.88) ^ {((1/12) * t)} V (96) = $ 4050`