From the task data
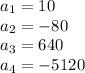
.
If these four terms form the geometrical sequence, then each next term is obtained from the previous by multiplying by the same number q.
Let's find q:
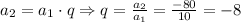
(you can easily check that q is also
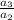
and
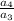
).
Then then-th term of geometrical sequence may be represented as
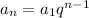
. That's why
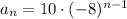
.