If the polynomial function
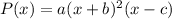
has a multiplicity of 2 at the point (−1, 0) then the factor (x-(-1))=(x+1) twice enters the polynomial representation. So, you have known one part of the left side of the polynomial function that is
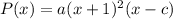
.
If polynomial function passes through the point (7,0), then
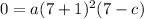
and since
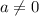
you have that c=7.
At last, if polynomial function passes through the point (0,-14), then

and
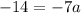
, so a=2.
Answer: a=2.