The polynomial
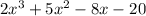
may have solutions which are the divisors of -20, therefore -20 has the following divisors:
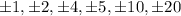
.
If x=1, then
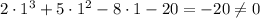
,
if x=-1, then

,
if x=2, then
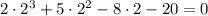
, then x=2 is a solution and you have the first factor (x-2).
If x=-2, then
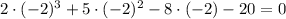
, then x=-2 is a solution, so you have the second factor (x+2).
Since x-2 and x+2 are two factors of
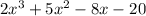
, then the polynomial
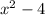
is a divisor of
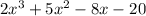
and dividing the polynomial
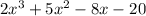
by
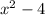
you obtain
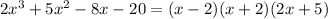
.