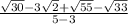Answer
Step-by-step explanation
Since we have radicals in the denominator, we need to rationalize our expression. To do it we just need to multiply both numerator and denominator by the conjugate of the denominator. Remember that the conjugate of a binomial is the same binomial with the sing in between changed.
Let's get our hands dirty:
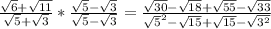
Now, we can simplify the denominator:
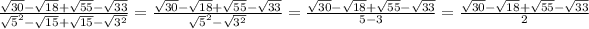
The only radical that we can simplify in the numerator is
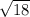 , which simplifies to:
, which simplifies to:
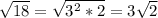
So, our final quotient is: