The best thing to do here is to put this into vertex form to first determine the vertex of the parabola. It is a positive parabola so it opens upwards, like a cup. To put it into vertex form we will complete the square. Move the 15 over to the other side by subtraction to isolate the x terms.
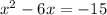
. Now we will take half the linear term, square it, and then add it to both sides. Our linear term is 6. Half of 6 is 3, and 3 squared is 9. So we add 9 to both sides and simplify the right side at the same time.
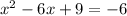
. During this process we have created a perfect square binomial on the left and it is within that binomial that we will find the h coordinate of the vertex. It's important for the focus.
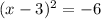
. Now bring the -6 back over by addition to get the k coordinate of the vertex.

. From this we see our (h, k) are (3, 6). The formula for the focus is
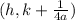
. Since our original parabola did not have a leading coefficient other than a 1, then our "a" is 1. Filling in the formula we have a focus at
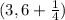
. Doing the addition inside there we simplify to
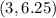
. That means that our focus is 1/4 of a unit above the vertex. So the focus is (3, 6.25). The directrix is the same distance from the vertex that the focus is, only it's the other direction. Our directrix will be 1/4 unit below the vertex and is a horizontal line, which is an equation in the form "y = ". Therefore,
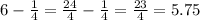
. That means that the equation for the directrix is y = 5.75.