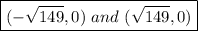Question

Find the vertices and locate the foci for the hyperbola whose equation is given. 49x2 - 100y2 = 4900

Answer 1

A hyperbola is the set of all points in a plane such that the difference of whose distances from two distinct fixed points called foci is a positive constant. In this problem, we have the following equation:

`49x^2-100y^2=4900`

What if we divide the whole equation by
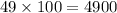`49 * 100=4900`? Well the result is:

`(1)/(4900)(49x^2-100y^2=4900) \\ \\ (49x^2)/(4900)-(100y^2)/(4900)=(4900)/(4900) \\ \\ (x^2)/(100)-(y^2)/(49)=1 \\ \\ \boxed{(x^2)/(10^2)-(y^2)/(7^2)=1}`

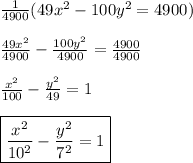
The standard form of the equation of the hyperbola given that the vertex lies on the origin is:

`(x^2)/(a^2)-(y^2)/(b^2)=1`

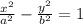
SO THE VERTICES ARE:

`\boxed{(a,0)=(10,0) \ and \ (-a,0)=(-10,0)}`

Calculating the foci:

`We \ know \ that \ foci \ are: \\ \\ (-c,0) \ and \ (c.0) \\ \\ Also: \\ \\ c=√(a^2+b^2) \\ \\ c=√(100+49) \therefore c=√(149)`

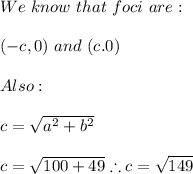
SO THE FOCI ARE:

`\boxed{(-√(149),0) \ and \ (√(149),0)}`