Question

Which equation is a line of symmetry for the graph shown

Answer 1

for a line, a symmetric line is any perpendicular line to it, because if you drop a perpendicular line, the line on one side is just a reflection of the other side.

so, in short, what is a likely equation of a line perpendicular to that one?

well, what's the slope of the line on the graph anyway? well, notice, we have a point of (-3,-4), let's pick another point on the line to get its slope, hmmm say (0,8),


`\bf (\stackrel{x_1}{-3}~,~\stackrel{y_1}{-4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ % slope = m slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{8-(-4)}{0-(-3)}\implies \cfrac{8+4}{0+3}\implies \cfrac{12}{3}\implies 4`


`\bf \stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{4\implies \cfrac{4}{1}}\qquad \qquad \qquad \stackrel{reciprocal}{\cfrac{1}{4}}\qquad \stackrel{negative~reciprocal}{-\cfrac{1}{4}}}`

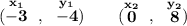
so, a line whose slope is -1/4 is a likely line of symmetry for that line, since it'd be a perpendicular line to it, and since you know your slope-intercept forms, you know which one that is.