Answer:
1. Reflection.
2. The scale factor is
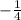 .
.
3. The coordinates of A' are (-9,4).
Explanation:
1. The hexagon on the right is the image of the hexagon on the left.
Both figures has same size and shape. The graph is symmetrical about the y-axis. Therefore the graph is reflected about the y-axis.
Hence, the correct option is 4.
2. The given dilation is
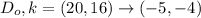
The scale factor is

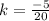
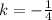
The scale factor is
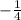 .
.
3. The point A (3, 4) is reflected over the line x = 2, and then is reflected over the line x = -4.
If a point reflected over the line x = 2, then

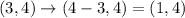
If a point reflected over the line x = -4, then
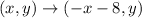
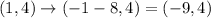
Therefore the coordinates of A' are (-9,4).