Question

What are the solutions to the equation 4x 3 - 5x = |4x|? List your answers in increasing order.

Answer 1

-1/2, 0, 3/2


this should be the answer, hopefully helped

Answer 2

Answer: The solutions of the given equation in increasing order are

`x=-(1)/(2),~0,~(3)/(2).`

Step-by-step explanation: The given equation is

`4x^3-5x=|4x|~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We are to solve the above equation and to list the solutions in increasing order.

We know that

`|x|=a~~~~~~\Rightarrow a=x~~\textup{or}~~a=-x.`

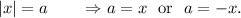
So, from equation (i), we get

`4x^3-5x=4x~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(iii)\\\\\textup{or}\\\\4x^3-5x=-4x~~~~~~~~~~~~~~~~~~~~~~~~~~~~(iv)`

Solving equation (iii), we get

`4x^3-5x=4x\\\\\Rightarrow 4x^3-9x=0\\\\\Rightarrow x(4x^2-9)=0\\\\\Rightarrow x=0,~~4x^2-9=0~~\Rightarrow x^2=(9)/(4)~~\Rightarrow x=\pm(3)/(2).`

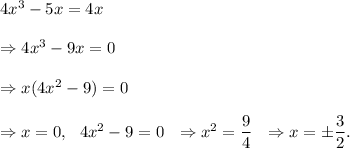
So, solutions of equation (i) are
`x=0,~(3)/(2),~-(3)/(2).`

And, solving equation (iv), we get

`4x^3-5x=-4x\\\\\Rightarrow 4x^3-x=0\\\\\Rightarrow x(4x^2-1)=0\\\\\Rightarrow x=0,~~~4x^2-1=0~~\Rightarrow x^2=(1)/(4)~~~\Rightarrow x=\pm(1)/(2).`

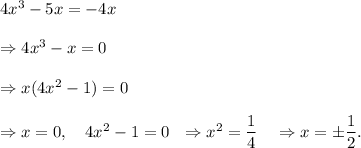
So, solutions of equation (ii) are
`x=0,~(1)/(2),~-(1)/(2).`

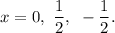
We can see that
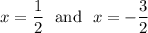`x=(1)/(2)~~\textup{and}~~x=-(3)/(2)` does not satisfy equation (i).

For
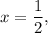`x=(1)/(2),` we have

`L.H.S.=4*(1)/(8)-5*(1)/(2)=-2,\\\\R.H.S.=|4*(1)/(2)|=2\\eq L.H.S.`

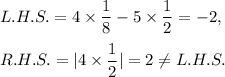
Similarly, for
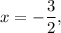`x=-(3)/(2),` we have

`L.H.S.=4* -(27)/(8)+5*(3)/(2)=-6,\\\\R.H.S.=|4* -(3)/(2)|=6\\eq L.H.S.`

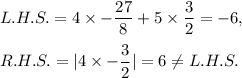
Thus, the solutions of the given equation in increasing order are

`x=-(1)/(2),~0,~(3)/(2).`