Question

Why is it necessary to use the absolute value of the difference when finding the distance on a number line, but not necessary when finding the differences of the coordinates in the coordinate plane?"

Answer 1

Remember that the distance on a number line is given by the formula:
`d=|x_(2)-x_(1)|`
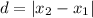
where

`d` is the distance between the points.

`x_(2)` is the second point in the number line.

`x_(1)` is the first point in the number line.
Now, suppose we are trying to find the distance between the points -1 and -5; our first point is -1, so
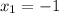
`x_(1)=-1`, and our second point is
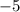
`-5`, so
`x_(2)=-5`. Suppose we are going to find the distance between the two point without using absolute value:

`d=x_(2)-x_(1)`

`d=-5-(-1)`

`d=-5+1`

`d=-4`
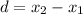
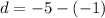
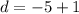
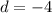
Look what we have here, a negative distance! Since distances cannot be negative, we must use absolute value to always get postie distances between two point on a umber line:

`d=|x_(2)-x_(1)|`

`d=|-5-(-1)|`

`d=|-5+1|`

`d=|-4|`

`d=4`

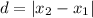
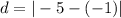
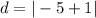
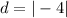
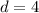
Now, the distance between two coordinates on a plane is given by the formula:
`d= \sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

`where`

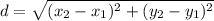
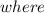
`d` is the distance between the two coordinates

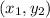
`(x_(1),y_(2))` are the coordinates of the first point

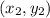
`(x_(2),y_(2))` are the coordinates of the second point
Notice that
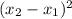
`(x_(2)-x_(1))^2` and
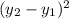
`(y_(2)-y_(1))^2` are squared, so it doesn't matter if we get a negative distance because a negative number raised to an even power (like 2) is always positive; therefore we don't need absolute value in this case because we won't ever get a negative distance.