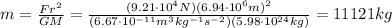The gravitational attraction between the Earth and the Hubble telescope is given by:
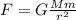
where
G is the gravitational constant
M is the Earth's mass
m is the Hubble mass
r is the distance of the Hubble telescope from the earth's center
By rearranging the equation and substituting the numbers given by the problem, we find the mass of the telescope: