Question

the function f(x) = 75(1.2)x models the number of rainbow trout in the lake x years after 2005 . approximately how many trout were in the lake in 2014

Answer 1

First, we are going to find the number of years form 2005 to 2014; to do it, we are going to subtract 2005 from 20014:
Number of years = 2014 - 2005 = 9 years

Now, we are going to replace
`x` with 9 in our function:

`f(x)=75(1.2)^x`

`f(x)=75(1.2)^9`

`f(x)=386.98`
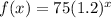
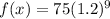
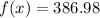
Rounded to the nearest integer:

`f(x)=387`

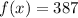
We can conclude that in the year 2014 will be approximately 387 rainbow tout in the lake.