Question

Suppose f(x)=x^2 and g(x)=(1/3X)^2. Which statement best compares the graph of g(x) with the graph of f(x)?

A. The graph of g(x) is the graph of f(x) shifted 1/3 units right.
B. The graph of g(x) is the graph of g(x) is the graph of f(x) horizontally stretched by a factor of 3.
C. The graph of g(x) is the graph of f(x) vertically stretched by a factor of 3.
D. The graph of g(x) is the graph of f(x) horizontally compressed by a factor of 3.

Answer 1

Vertically compressed by 1/9 not 3

Explanation:

See picture attached to see comparison. The parent graph is black and the new graph is red. By adding 1/3 to the graph, the parabola becomes more compressed and wider. It is vertically compressed to become wider.

Answer 2

B. The graph of g(x) is the graph of g(x) is the graph of f(x) horizontally stretched by a factor of 3.

Explanation:

Horizontal shifting right by c units,

`(x,y)\rightarrow (x-c,y)`

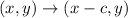
Horizontally stretched by factor c.

`(x,y)\rightarrow ((x)/(c),y)`

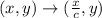
Vertically stretched by factor c. ( where, 0< |c|<1 )

`(x,y)\rightarrow (x,cy)`

Horizontally compressed by a factor of c. ( where, |b| > 1 )

`(x,y)\rightarrow (cx,y)`

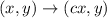
Here,

`f(x) = x^2`

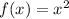
When f(x) is shifted 1/3 unit right,

Then, the transformed function is,

`g(x) = (x-(1)/(3))^2`

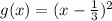
When f(x) is stretched horizontally by the factor of 3,

Then, the transformed function is,

`g(x)=((1)/(3)x)^2`

When, f(x) vertically stretched by a factor of 3,

Then, the transformed function is,

`g(x)=3(x)^2`

When, f(x) is horizontally compressed by a factor of 3,

Then, the transformed function is,

`g(x)=(3x)^2`

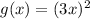
Hence, option B is correct.