Answer:
Line LM is perpendicular to line AB. It's equation is 5y - 6x = 15
Explanation:
Given: Slope of line, AB
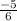
To find: A line which is perpendicular to given line AB
We know that if two lines are perpendicular than product of their slope is -1.
Let slope of required line is m then by using given condition we get,

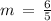
Now we check slope of each and every line and matches with value of m.
using two point we find slope.
formula for slope,
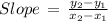
Coordinates of Given points are P( -5 , 4 ) , Q( 0 , -2 ) , J( -6 , 1 ) , K( 0 , -4 ) ,
L( -5 , -3 ) , M( 0 , 3 ) , N( -6 , -5 ) and O( 0 , 0 )
Slope of line PQ =
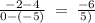
Slope line JL =
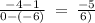
Slope line LM =
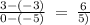
Slope line NO =
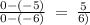
Thus, By comparing with above slope.
LM is our required line which is perpendicular to given Line AB.
For equation we use point-slope form,
Equation line LM

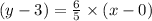
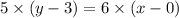
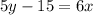
5y - 6x = 15
Therefore, Line LM is perpendicular to line AB. It's equation is 5y - 6x = 15