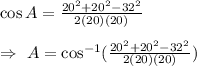Question

PLEASE HELP ASAP!!!!!!!!!!

A contractor wants to design a triangular window as shown below.



Which expression below is equivalent to the angle that must be formed at the apex of the window?

I put the answer options in the Pictures below please choose from them

Answer 1

Answer: cos -1 (20 2 + 20 2 -32 2 / 2(20)(20)

Explanation:

Answer 2

Answer:
`\cos^(-1)((20^2+20^2-32^2)/(2(20)(20)))`

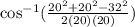
Explanation:

Cosine Rule:

`\cos A=(b^2+c^2-a^2)/(2bc)`

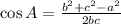
In the given picture , there is an isosceles triangle with equal sides as 20 in and altitude =12.

We know that the altitude of a isosceles triangle divides the base of triangle in two equal halves.

Consider, half of triangle i.e. right triangle with hypotenuse 20 in. and perpendicular 12 in.

Let 'x' be the base of the right triangle.

Then by Pythagoras theorem ,

`x^2=(20)^2+(12)^2=400-144=256\\\\\Rightarrow\ x=16`

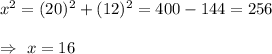
Now, the base of the whole triangle (a)=
`2(16)=32`

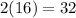
Let A be the angle formed at the apex of the window, then by law of cosines we have

`\cos A=(20^2+20^2-32^2)/(2(20)(20))\\\\\Rightarrow\ A=\cos^(-1)((20^2+20^2-32^2)/(2(20)(20)))`