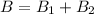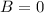Answer:
ZERO
Step-by-step explanation:
As we know that magnetic field due to a straight wire at some distance from the wire is given as

so here since we have to find the magnetic field at the mid point of two parallel wire having equal current in them
so we can say
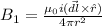
and since it is mid of of two wires so all the parameters will be same but the direction would be reversed as the mid point lies on the right side of one wire and on the left side of other wire.
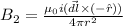
now net magnetic field at mid point will be