Question

A player kicks a soccer ball from ground level and sends it flying at an angle of 30 degrees at a speed of 26 m/s. What is the maximum height attained by the ball? Round to the nearest tenth of a meter.

Answer 1

By definition, the height is given by:

`h (t) = (1/2) * (a) * (t ^ 2) + v0 * t + h0`
Where,
a: acceleration
v0: initial speed
h0: initial height.
The initial velocity in its vertical component is:

`v0 = 26 * sine (36) v0 = 15.3 m / s`
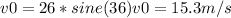
The initial height is:

`h0 = 0 m` (the ball is on the ground)
The acceleration is:

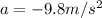
`a = -9.8 m / s ^ 2` (acceleration of gravity)
Substituting values:

`h (t) = (1/2) * (- 10) * (t ^ 2) + 15.3 * t + 0`
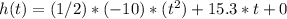
Rewriting:

`h (t) = -4.9 * t ^ 2 + 15.3 * t`
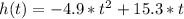
The time in which the maximum height occurs is obtained by deriving:

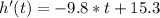
`h '(t) = -9.8 * t + 15.3` We set zero and let's time:

`-9.8 * t + 15.3 = 0 t = 15.3 / 9.8 t = 1.56`
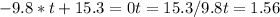
We evaluate the time obtained in the equation of the height, to obtain the maximum height:

`h (1.56) = -4.9 * (1.56) ^ 2 + 15.3 * (1.56) h (1.56) = 11.9 m`
Answer:
The maximum height attained by the ball is:
h (1.56) = 11.9 m