Answer:
The sculpture of the woman must be 268 inches tall.
Explanation:
This problem is about proportions and scales factors.
According to the problem, a sculpture of a clothespin is 20 feet, and a normal clothespin is 5 inches high.
So, the ratio is
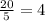
If a woman is 5 feet and 7 inches, the height of her sculpture must be in the given ratio.
First, we need to use only inches units. We know that 1 foot is 12 inches.

So, the woman height is 67 inches.
Using the given scale factor, we multiply it with the height of the woman
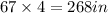
Therefore, the sculpture of the woman must be 268 inches tall.