Question

Please help asap...

Answer 1

Hey!


I know this is just one problem, but I'm going to explain how to solve each separately and how to tell if two equations are inverse.

EQUATION NUMBER 1 :

Problem :
f ( x ) =
`(x-4)/(-7)`

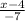
A simple, easy way to solving this problem would be to get rid of the f ( x ) = part. After that's gone, move the negative symbol for negative 7 to the left of the whole equation.

Original Problem :
f ( x ) =
`(x - 4)/(-7)`

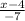New Equation {Solved by Placing a Negative to the Left of the Equation} :
-
`(x - 4)/(7)`

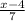So, this means our answer for f ( x ) =
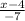`(x - 4)/(-7)` is -
`(x-4)/(7)` .

BONUS:

The slope of the answer is -
`(1)/(7)`



EQUATION NUMBER 2 :

Problem :
g ( x ) = -7x + 4

This equation here is already at its simplest form and cannot be simplified any farther.

So, this equation will stay just as it is.



ARE THEY INVERSE? :

If you want to find out if an equation is inverse, here's how you can tell...

If a function f ( x ) is mapping x to y, then the inverse function of that should map y back to x.

This may sound complicated, but it's fairley simple.

When we simplified the first equation in problem one, we got the equation for problem two. That was a major hint that it could be the inverse equation.

Also, judging by the two equations, you can tell that the f ( x ) function would map from y to x.

This means both equations are inverse.

Hope I helped!


- Lindsey Frazier ♥