Question

You are designing a miniature golf course and need to calculate the surface area and volume of many of the objects that will be used to build the course. a. The first hole has a sphere that has a radius of 5 feet. What is the surface area and volume of the sphere? b. The fourth hole has a pyramid that has a height of 12 feet; the base is a square with sides that measure 8 feet. What is the surface area and volume of the pyramid? c. The seventh hole has a cone that has a height of 8 feet; the base has a radius of 5 feet. What is the surface area and volume of the cone? d. The fourteenth hole has a rectangular solid that measures 10 feet long, 6 feet wide, and 16 feet tall. What is the surface are and volume of the rectangular solid? e. Your boss wants to place signs on each face of the structures. How many faces are on the four geometric shapes on the holes? f. To meet building codes we need to know the number of edges to place the appropriate brackets. How many edges will need brackets on the four shapes? g. For extra support we also need to place additional brackets at each vertex. How many vertices are there for each structure?

Answer 1

a. To solve the first part, we are going to use the formula for the surface area of a sphere:
`A=4 \pi r^2`
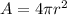
where

`A` is the surface area of the sphere

`r` is the radius of the sphere
We know from our problem that
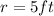
`r=5ft`; so lets replace that value in our formula:

`A=4 \pi (5ft)^2`

`A=314.16ft^2`

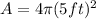
To solve the second part, we are going to use the formula for the volume of a sphere:
`V= (4)/(3) \pi r^3`
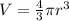
Where

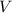
`V` is the volume of the sphere

`r` is the radius
We know form our problem that
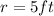
`r=5ft`, so lets replace that in our formula:

`V= (4)/(3) \pi (5ft)^3`

`V=523.6ft^3`

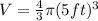
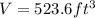We can conclude that the surface area of the sphere is 314.16 square feet and its volume is 523.6 cubic feet.

b. To solve the first part, we are going to use the formula for the surface area of a square pyramid:
`A=a^2+2a \sqrt{ (a^2)/(4) +h^2}`
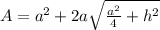
where

`A` is the surface area

`a` is the measure of the base

`h` is the height of the pyramid
We know form our problem that
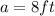
`a=8ft` and
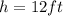
`h=12ft`, so lets replace those value sin our formula:

`A=(8ft)^2+2(8ft) \sqrt{ ((8ft)^2)/(4) +(12ft)^2}`

`A=266.39ft^2`

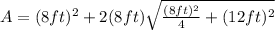
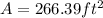
To solve the second part, we are going to use the formula for the volume of a square pyramid:
`V=a^2 (h)/(3)`
where

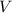
`V` is the volume

`a` is the measure of the base

`h` is the height of the pyramid
We know form our problem that
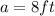
`a=8ft` and
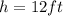
`h=12ft`, so lets replace those value sin our formula:

`V=(8ft)^2 ((12ft))/(3)`

`V=256ft^3`

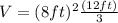
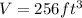We can conclude that the surface area of our pyramid is 266.39 square feet and its volume is 256 cubic feet.

c. To solve the first part, we are going to use the formula for the surface area of a circular cone:
`A= \pi r(r+ √(h^2+r^2)`
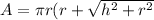
where

`A` is the surface area

`r` is the radius of the circular base

`h` is the height of the cone
We know form our problem that
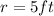
`r=5ft` and
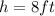
`h=8ft`, so lets replace those values in our formula:

`A= \pi (5ft)[(5ft)+ √((8ft)^2+(5ft)^2)]`

`A=226.73ft^2`

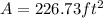
To solve the second part, we are going to use the formula for the volume os a circular cone:
`V= \pi r^2 (h)/(3)`
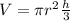
where

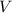
`V` is the volume

`r` is the radius of the circular base

`h` is the height of the cone
We know form our problem that
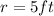
`r=5ft` and
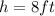
`h=8ft`, so lets replace those values in our formula:

`V= \pi (5ft)^2 ((8ft))/(3)`

`V=209.44ft^3`

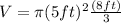
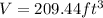We can conclude that the surface area of our cone is 226.73 square feet and its surface area is 209.44 cubic feet.

d. To solve the first part, we are going to use the formula for the surface area of a rectangular prism:
`A=2(wl+hl+hw)`
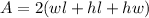
where

`A` is the surface area

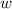
`w` is the width

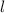
`l` is the length

`h` is the height
We know from our problem that
`w=6ft`,
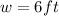
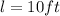
`l=10ft`, and
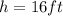
`h=16ft`, so lets replace those values in our formula:

`A=2[(6ft)(10ft)+(16ft)(10ft)+(16ft)(6ft)]`

`A=632ft^2`

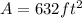
To solve the second part, we are going to use the formula for the volume of a rectangular prism:
`V=whl`
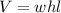
where

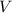
`V` is the volume

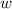
`w` is the width

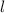
`l` is the length

`h` is the height
We know from our problem that
`w=6ft`,
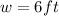
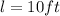
`l=10ft`, and
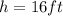
`h=16ft`, so lets replace those values in our formula:

`V=(6ft)(16ft)(10ft)`

`V=960ft^3`

We can conclude that the surface area of our solid is 632 square feet and its volume is 960 cubic feet.

e. Remember that a face of a polygon is a side of polygon.
- A sphere has no faces.
- A square pyramid has 5 faces.
- A cone has 1 face.
- A rectangular prism has 6 faces.
Total faces: 5 + 1 + 6 = 12 faces

We can conclude that there are 12 faces in on the four geometric shapes on the holes.

f. Remember that an edge is a line segment on the boundary of the polygon.
- A sphere has no edges.
- A cone has no edges.
- A rectangular pyramid has 8 edges.
- A rectangular prism has 12 edges.
Total edges: 8 + 20 = 20 edges

Since we have 20 edges in total, we can conclude that your boss will need 20 brackets on the four shapes.

g. Remember that the vertices are the corner points of a polygon.
- A sphere has no vertices.
- A cone has no vertices.
- A rectangular pyramid has 5 vertices.
- A rectangular prism has 8 vertices.
Total vertices: 5 + 8 = 13 vertices

We can conclude that there are 0 vertices for the sphere and the cone; there are 5 vertices for the pyramid, and there are are 8 vertices for the solid (rectangular prism). We can also conclude that your boss will need 13 brackets for the vertices of the four figures.