Question

If the discriminant of a quadratic equation is positive, which of the following is true of the equation?

A. it has two complex solution

B. it has two real solutions

C. it has one real solution

Answer 1

it is b. it has two real solutions.

Explanation:

Answer 2

For this case suppose that we have a quadratic equation of the form:

`ax ^ 2 + bx + c`
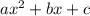
The solution to the quadratic recuacion is given by:

`x = (-b +/- √(b^2 - 4ac))/(2a)`
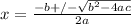
Where,
The discriminant is:

`b ^ 2 - 4ac`
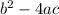
When the discriminant is greater than zero, then the root is positive, and therefore, we have two positive real solutions.
Answer:
B. it has two real solutions