Answer:
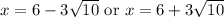
Explanation:
We have been given an equation
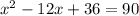 . We are asked to solve for x in our given equation.
. We are asked to solve for x in our given equation.
We can see that left side of our given equation is a perfect square.
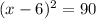
We will take square root of both sides of our given equation to solve for x.
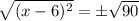
Using radical rule
![\sqrt[n]{a^n}=a](https://img.qammunity.org/2019/formulas/mathematics/middle-school/c3rtlwkabi5hdv4iqwjzk5hvo0m9e91u35.png) , we will get:
, we will get:
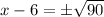
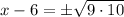
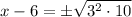

Using radical rule
![\sqrt[n]{a^n}=a](https://img.qammunity.org/2019/formulas/mathematics/middle-school/c3rtlwkabi5hdv4iqwjzk5hvo0m9e91u35.png) , we will get:
, we will get:
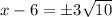
Now, we will add 6 on both sides of our given equation as:
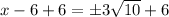
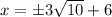
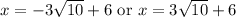
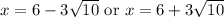
Therefore, the solution for our given equation would be
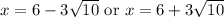 .
.