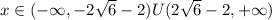Question

the graph of the parabola y=1/4(x+2)^2-6 is shown on the coordinate plane below according to the graph for which values of x is y always positive ?

Answer 1

Answer: x∈(-∞,-2√6-2)U(2√6-2,+∞)

Explanation:

`\displaystyle\\y=(1)/(4) (x+2)^2-6\\y > 0\\Hence,\\(1)/(4)(x+2)^2-6 > 0 \\\\(1)/(4)(x+2)^2-6+6 > 0+6\\\\(1)/(4)(x+2)^2 > 6\\`

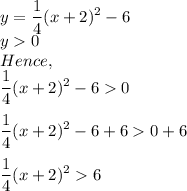
Multiply both parts of the equation by 4:

`(x+2)^2 > 24`

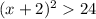
Extract the square root of both parts of the inequality:

`|x+2| > √(24) \\|x+2| > √(4*6) \\|x+2| > 2√(6)`

Expand the modulus - we get a set of inequalities:

`\displaystyle\\\left [{{x+2 > 2√(6)\ \ \ \ (1) } \atop {-(x+2) > 2√(6) \ \ \ (2)}} \right.\\`

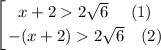
Multiply both parts of inequality (2) by -1 and reverse the sign of the inequality:

`\displaystyle\\\left [ {{x+2-2 > 2√(6)-2 } \atop {x+2 < -2√(6) }} \right. \ \ \ \ \ \left [ {{x > 2√(6)-2 } \atop {x+2-2 < -2√(6) -2}} \right. \ \ \ \ \ \left [ {{x > 2√(6)-2 } \atop {x < -2√(6)-2 }} \right.`

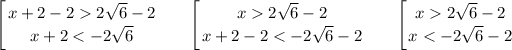
Thus,

`x\in(-\infty,-2√(6)-2)U(2√(6) -2,+\infty)`