Question

A spinner has regions numbered 1 through 21. what is the probability that the spinner will stop on an even number or a multiple of 3

Answer 1

Answer:
`(2)/(3)`

Explanation:

Given : The total number of regions in the spinner = 21

The outcomes for even number =2,4,6,8,10,12,14,16,18,20

The outcomes for multiple of 3 = 3,6,9,12,15,18,21

The number of outcomes of getting an even number or a multiple of 3 = 14

Then, the probability that the spinner will stop on an even number or a multiple of 3 will be :-

`(14)/(21)=(2)/(3)`

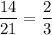
Hence, the probability that the spinner will stop on an even number or a multiple of 3 is
`(2)/(3)`

Answer 2

10 of the numbers are even. 4 more are odd multiples of 3. The probability of landing on even or a multiple of 3 is (10+4)/21 = 2/3.