General formula to find the area of a circle

To find a sector area of a circle

NUMBER 14
Given information:
r = 12 cm
degree of sector = 110° (use the angle on the shaded area)
The area of the sector:
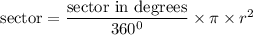
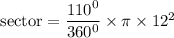
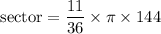

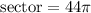
sector = 44 × 3.14
sector = 138.16
The area is 44π ≈ 138.16 cm²NUMBER 16Given information:
r = 30 yards
degree of sector = 15° (use the angle on the shaded area)
The area of the sector:
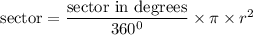
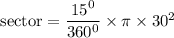

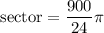

sector = 37.5 × 3.14
sector = 117.75
The area is 37.5π ≈ 117.75 yd²