Question

Complete the square to rewrite y = x^2 + 6x + 3 in vertex form. Then state whether the vertex is a maximum or a minimum and give its coordinates.

A. Maximum at (–3, –6)
B. Minimum at (3, –6)
C. Minimum at (–3, –6)
D. Maximum at (3, –6)

Answer 1

First of all, we convert the equation to a vertex form.

`y = x^(2)+6x+3`

`y=(x^(2)+6x)+3`

`y = (x+3)^(2)+3-9`

`y = (x+3)^(2)-6`.
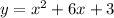
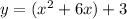
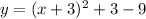
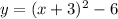
The equation in vertex form is
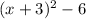
`(x+3)^(2)-6`. By looking at the equation we can understand that the y value of the vertex point is -6. By further calculation we can verify that the x value of the vertex point is -3.
Now, there are two ways of finding if the vertex point is a maximum or a minimum. The first way is picking random x coordinates after and before the y vertex value. If the values of y decrease before the y vertex point and increase afterwards, the vertex is a minimum. If the values of y increase before the y vertex point and then decrease afterwards, the vertex is a maximum point. The second way is applying teh second derivative. Here, I will show you the way of doing it:

`y = x^(2) + 6x +3`

`(dy)/(dx) = 2x + 6`

`(d^(2)y)/(dx^2) = 2`
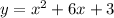
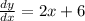
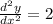
The result proves two facts about the function:
1. The function has only one vertex/turning point.
2. The vertex/turning point is a minimum (due to the result of the second derivative being positive).

The answer is C.