Question

Are these fractions equivalent or nonequivalent?

4m/5n

8m/10n

I'm thinking no since you can't divide them all by one number?? I'm just trying to make sure I'm right

Answer 1

To compare whether or not two fractions are equivalent, they must have the same denominator.

What is a common denominator you can make between
`(4m)/(5n)` and
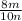
`(8m)/(10n)`? Some possible options are 5n or 10n.

I'll make both denominators 5n:
1)
`(4m)/(5n)` already has 5n in the denominator.
2) To get 5n in the denominator for
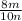
`(8m)/(10n)`, you want to divide both the numerator and denominator by 2 (same as multiplying top and bottom by
`(1)/(2)`). Since you're doing the same thing to the numerator and denominator, you are not changing the value of the fraction:

`(8m)/(10n) * ( (1)/(2))/((1)/(2)) \\ = ( (8m)/(2))/((10n)/(2))\\ = (4m)/(5n)`

Now compare the two fractions. Since
`(4m)/(5n) = (4m)/(5n)`, your fractions are equivalent!

-------

Answer: They are equivalent