For this case we have the following functions:
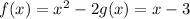
We must make the following composition of functions:

This composition of functions means that we must replace the function g (x) in the function f (x) in the following way:
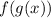
We have then:
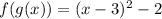
Rewriting we have:
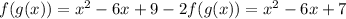 Answer:
Answer:
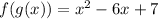 option 2
option 2