Question

Please explain and/or show your work!! :)

Answer 1

>> Answer

_________

`\:`

Answer in the picture.

Answer 2

`\left[ \begin{matrix} 2 & a \\ -1 & -2 \end{matrix} \right] + \left[ \begin{matrix} b & 4 \\ -2 & 1 \end{matrix} \right]`

This addition of matrices can be combined into one matrix.
To add matrices, add the corresponding components of each matrix.

After adding, we'll have the following


`\left[ \begin{matrix} 2+b & a+4 \\ -3 & -1 \end{matrix} \right]`

This matrix should be equal to the matrix on the right-hand side of the equation. This means that each corresponding component of this matrix and the other matrix should be equivalent.

This means that


`2+b=1`
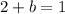
AND

`a+4=0`

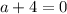
Solving these one-step equations will give the values of a = -4 and b = -1. That's answer choice D.