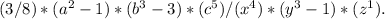Final answer:
The expression simplifies to
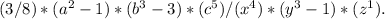
Step-by-step explanation:
To rewrite the expression (3a^2b^3c^5)/(8x^4y^3z) without a denominator, we need to eliminate the fraction. This can be done by multiplying the numerator and denominator by the reciprocal of the denominator.
The expression becomes
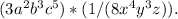
Next, we can simplify the expression by multiplying the numerators together and multiplying the denominators together.
This gives us
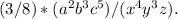
The final step is to simplify the expression by dividing the coefficients and subtracting the exponents of the variables.
The expression simplifies to